6. コヒーレントフォノン制御
固体結晶に対し、そのフォノン振動の周期よりも短い時間幅を持ったパルスレーザーを照射すると、結晶のフォノン運動を励起することができる。通常の熱で励起されるフォノンと異なり、 レーザー光が照射された領域内で原子(分子)の運動の位相が揃った状態で励起が行われるため、このようなフォノン振動をコヒーレントフォノンと呼ぶ。 コヒーレントフォノンを計測するには、pump-probe分光によって反射率の変化として計測することが一般的です。
6-1. ビスマス単結晶の二次元原子運動の制御と可視化
ビスマスの単位格子を図11に示す。z軸方向に振動するA1gモードとxy平面内で二重縮退したEgモードという二つのモードが存在して�いる。 これらのモードの励起振幅を光によって制御することができれば、結晶格子中の原子の運動を制御できることに繋がる。実験では、図12のような光学系を用い、ポンプ光の照射による プローブ光の反射率変化を測定している。

図11 ビスマスの単位格子とフォノンモード

図12 コヒーレントフォノン光学系
励起パルスとしてチャープパルスを時間的に重ねた励起パルスを用い、両者の遅延時間を制御することでTHz領域の変調をスペクトルに与え、フォノンの振幅制御をおこなっている。 さらにab initio計算によって反射率の変化と原子の変位の間の比例定数を計算し、反射率の変化から光の照射された平面内における原子の変位を可視化することに成功した。 より詳細を知りたい方は、以下の文献を参考にして下さい。
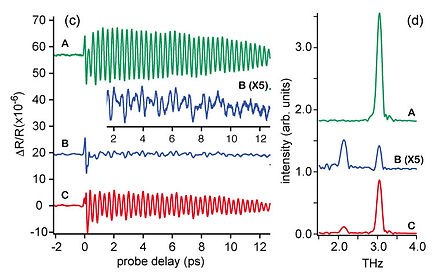
図13 フォノン振幅制御結果
6-2. ルブレン単結晶のTHzフォノン熱浴分布の制御
現在執筆中
【関連論文】
-
Optical manipulation of coherent phonons in superconducting YBa2Cu3O7-δ thin films
Y. Okano, H. Katsuki, Y. Nakagawa, H. Takahashi, K. G. Nakamura and K. Ohmori, Faraday Discussions 153, 375-382 (2011). -
All-Optical Control and Visualization of Ultrafast 2D Atomic Motions in a Single Crystal of Bismuth
H. Katsuki, J. C. Delagnes, K. Hosaka, K. Ishioka, H. Chiba, E. S. Zijlstra, M. E. Garcia, H. Takahashi, K. Watanabe, M. Kitajima, Y. Matsumoto, K. G. Nakamura, and K. Ohmori, Nature Communications 4:2801 doi:10.1038/ncomms3801 (2013). -
Mode Selective Excitation of THz vibrations in Single Crystalline Rubrene
K. Yano, H. Katsuki, and H. Yanagi,
J. Chem. Phys. 150, 054503 (2019).
2. コヒーレント制御とは?
コヒーレント制御とは、ターゲットとなる原子、分子系の量子状態を光のコヒーレンスを利用して制御する技術である。 光と物質の相互作用を利用して、光の持つコヒーレンスを系の波動関数に転写することができる。 光パルスの時間形状やスペクトルは、位相変調器や干渉計を利用したダブルパルス生成を利用して比較的簡単に制御することができるため、 このような光を用いることにより、系の波動関数の複雑な重ね合わせを外部から制御する事が可能になる。 我々の研究ではフェムト秒の超短パルスレーザー光を光源に用いる事により、対象とする系の固有関数の重ね合わせを作成し、その運動を 制御する事を目指している。 量子状態を記述する波動関数は振幅と位相から構成されており、それらのパラメータを自在に制御する事ができると、ポテンシャル状における波束の 運動を制御できる事になる。このような技術は、化学反応における反応生成物の分岐比制御や量子通信、計算における状態生成、制御などに おいて核心となる技術である。
ある系に対して、コヒーレント制御を行う上で最も必要とされる特徴は、「生成した量子状態が量子的な特徴を保ち続けていること」である。 光励起によって生成した量子状態は時間の経過とともに、周囲との相互作用などの結果 その量子的な特徴を徐々に失っていくことが知られている。(難しい言葉で位相緩和と言います。) コヒーレント制御で状態を制御できるのは、個々の状態が明確な位相を持っていて、それらを重ね合わせた結果も明確に定義できることが前提となっており、 もしそれぞれの状態の位相が不明瞭になってしまうと、足し合わせの結果もはっきりとしないものになってしまいます。
このような実験を行うにはコヒーレンスの良い光源、つまりレーザー光源が必要となります。我々のグループでは超短パルスレーザーを用いたコヒーレント制御を これまで行ってきました。 超短パルスレーザーは広いスペクトル幅を持っており、分子の持つ振動準位の間隔と比較して、十分バンド幅の広いレーザーを入射した場合、 複数の振動固有状態を同時に励起することができます。このような状態を数式で表すと、
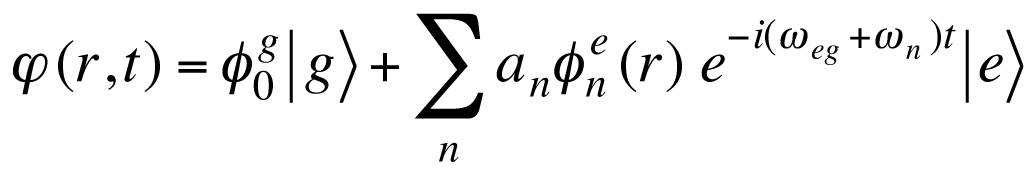
の様に表され、波束(wave packet)と呼ばれます。ここで、Φ0gは基底状態のv=0振動波動関数、Φneは励起状態のv=n振動波動関数、ωegは電子状態間の角周波数、ωnはv=n振動準位の角周波数、 anはv=n状態の振幅を表す。|g>と|e>はそれぞれ電子状態波動関数のブラケット表記である。 波束を構成する波動関数の種類によって、振動波束、電子波束、回転波束などと細分化されます。 以下に述べる私の研究では主に振動波束の運動を対象としています。 一次元の調和ポテンシャル中での典型的な振動波束の運動を以下に示します。表示されているのは波束密度です。
調和ポテンシャル中の振動波束の運動
横軸は二原子分子の核間距離に相当します。 波束が一周運動するのにかかる時間のことを古典振動周期(Tvib)と呼びます。実際の分子では、ポテンシャルは非調和性を含むので波束の運動はもう少し運動は複雑になり、 時間の経過とともに徐々に波束の形が崩れていくことになります。
次に二発の超短パルスレーザーを時間差τをつけて分子に照射した場合の、電子励起状態に生成される波束の運動を考えます。 励起強度が十分小さい場合には、基底状態のポピュレーションはほぼ1のま�まであると近似でき、生成される状態は
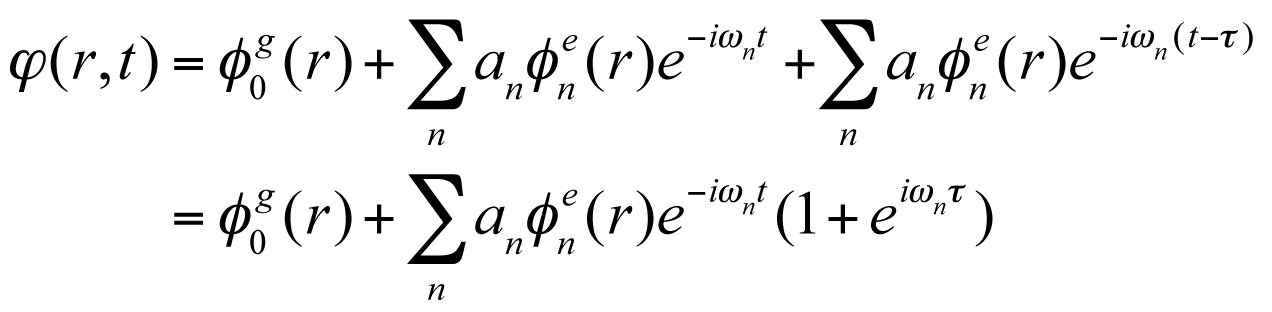
の様に表されます。ここで二乗をとって、ポピュレーションの分布を計算すると、
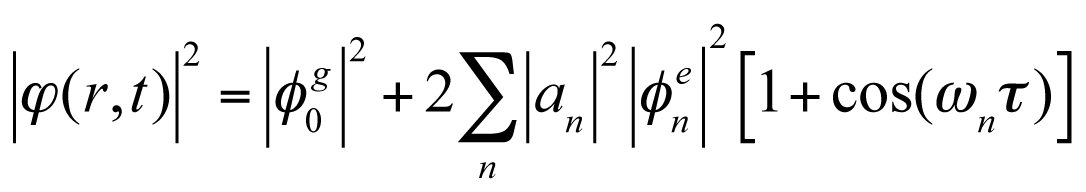
が得られる。この式で重要な点は、励起状態の各振動準位のポピュレーションがτの関数として、角振動数ωnで振動しているということです。 実際にヨウ素分子の実験を行った場合の条件で考えると、ヨウ素の電子振動励起はおよそ530nmの光で行っています。これからポピュレーションの振動周期を計算すると、 1.8×10 sとなり、非常に短い時間周期でポピュレーションが振動していることがわかります。この結果から、高い精度で各固有状態の ポピュレーション分布を制御するためには、非常に高い安定度でτを制御する必要があることがわかります。 実際に、二つの波束の重ね合わせの結果が最も強くなる場合と弱くなる場合について、シミュレートした結果を次に示します。
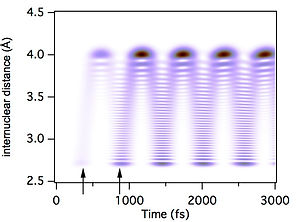
図2-1 (a) 波束の強め合い
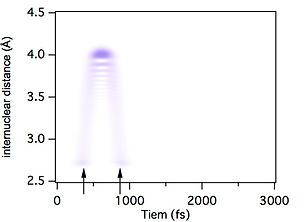
図2-1 (b) 波束の弱め合い
図中の矢印のタイミングがレーザー光が照射されるタイミングに相当します。以下では、一発目の励起パルスをポンプパルス、二発目の励起パルスをコントロールパルスと 呼びます。 左側の強め合いの場合にはτ=499.7fs、右側の弱め合いの場合にはτ=498.8fsとなっています。 たった0.9fsだけ、照射パルスのタイミングを変えることで、最終的に生成される波束の状態が劇的に変化していることがこの結果からわかります。 理想的な状態では、波を重ね合わせることで最終状態のポピュレーションは単パルス励起のときのポピュレーションの0から4倍までの間で振動することになります。
私の研究では、様々な量子系を対象としてその量子状態を制御することを研究しています。当然ですが、単純な系で量子状態の位相寿命が長いほど コヒーレント制御は容易に行えますが、起こる現象もある意味想定通りの現象でしかありません。図2-2に示すように、気相中の孤立分子からスタートして、現在はより複雑な固体系を対象としてその量子的な状態の制御に挑戦しています。 以下ではそれぞれの量子系におけるコヒーレント制御実験について紹介します。
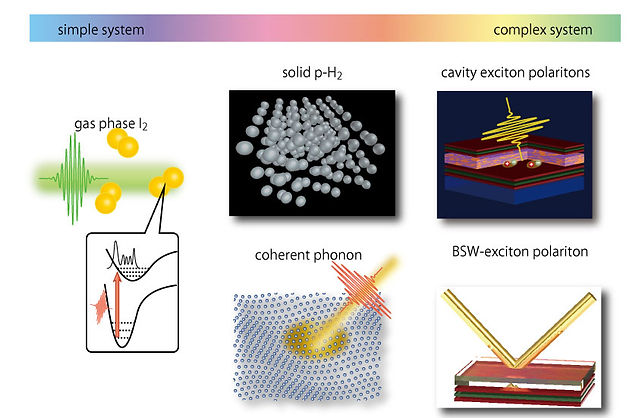
図2-2 コヒーレント制御の対象とする量子系
-15

