6. コヒーレントフォノン制御
固体結晶に対し、そのフォノン振動の周期よりも短い時間幅を持ったパルスレーザーを照射すると、結晶のフォノン運動を励起することができる。通常の熱で励起されるフォノンと異なり、 レーザー光が照射された領域内で原子(分子)の運動の位相が揃った状態で励起が行われるため、このようなフォノン振動をコヒーレントフォノンと呼ぶ。 コヒーレントフォノンを計測するには、pump-probe分光によって反射率の変化として計測することが一般的です。
6-1. ビスマス単結晶の二次元原子運動の制御と可視化
ビスマスの単位格子を図11に示す。z軸方向に振動するA1gモードとxy平面内で二重縮退したEgモードという二つのモードが存在して�いる。 これらのモードの励起振幅を光によって制御することができれば、結晶格子中の原子の運動を制御できることに繋がる。実験では、図12のような光学系を用い、ポンプ光の照射による プローブ光の反射率変化を測定している。

図11 ビスマスの単位格子とフォノンモード

図12 コヒーレントフォノン光学系
励起パルスとしてチャープパルスを時間的に重ねた励起パルスを用い、両者の遅延時間を制御することでTHz領域の変調をスペクトルに与え、フォノンの振幅制御をおこなっている。 さらにab initio計算によって反射率の変化と原子の変位の間の比例定数を計算し、反射率の変化から光の照射された平面内における原子の変位を可視化することに成功した。 より詳細を知りたい方は、以下の文献を参考にして下さい。
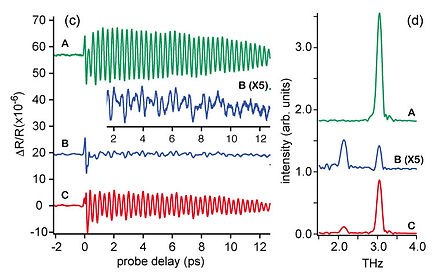
図13 フォノン振幅制御結果
6-2. ルブレン単結晶のTHzフォノン熱浴分布の制御
現在執筆中
【関連論文】
-
Optical manipulation of coherent phonons in superconducting YBa2Cu3O7-δ thin films
Y. Okano, H. Katsuki, Y. Nakagawa, H. Takahashi, K. G. Nakamura and K. Ohmori, Faraday Discussions 153, 375-382 (2011). -
All-Optical Control and Visualization of Ultrafast 2D Atomic Motions in a Single Crystal of Bismuth
H. Katsuki, J. C. Delagnes, K. Hosaka, K. Ishioka, H. Chiba, E. S. Zijlstra, M. E. Garcia, H. Takahashi, K. Watanabe, M. Kitajima, Y. Matsumoto, K. G. Nakamura, and K. Ohmori, Nature Communications 4:2801 doi:10.1038/ncomms3801 (2013). -
Mode Selective Excitation of THz vibrations in Single Crystalline Rubrene
K. Yano, H. Katsuki, and H. Yanagi,
J. Chem. Phys. 150, 054503 (2019).
4. 固体パラ水素中での振動回転状態制御
4-1. 非線形分光法を利用したコヒーレント状態の振幅制御
気相中の孤立分子よりも複雑な系として、次に固体パラ水素中での振動励起子制御について紹介する。水素分子はその核スピンの対称性からパラ水素とオルト水素に分類される。 パウリの排他則の結果、パラ(オルト)水素は回転量子数Jが偶数(奇数)しか取ることができない。結果的に、極低温で作成したパラ水素結晶中の水素分子はほぼすべてJ=0状態に 存在していると考えられる。J=0状態の固有関数は等方的�な分布を持っていることから、固体パラ水素では各分子が特定の軸方向を持っているのではなく、等方的な分布を持った球体のように 扱うことができ、希ガス結晶のようなイメージでとらえることが妥当である。(下図参照)さらに、電気的な多極子モーメントが存在しないことから、分子間の静電的な相互作用も非常に弱い。特に v=1←0の純粋振動遷移を考えると、分子の球対称性も維持されるために振動励起状態のコヒーレンス寿命が非常に長いという特徴を持つ。不純物濃度にもよるが、1ns程度のコヒーレンス 寿命を容易に得ることができる。

図4-1 パラ水素結晶の特徴
パラ水素結晶は多粒子系であるため、その波動関数は非常に多自由度の複雑なものとなる。個々の分子基底から出発すると、分子iがv=1に励起していてその他の分子がすべて基底状態 にあるような状態は
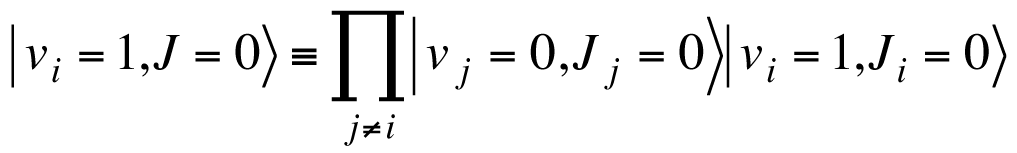
と表される。この状態を基底として、分子間相互作用を対角化することによって、非局在化した振動固有関数が得られ、次のように波数ベクトルkによってラベル付けされる。
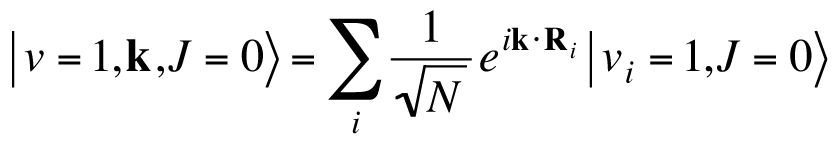
このような系を対象に、その振動励起状態の波束の重ね合わせによる波束干渉制御を行った。 実験のスキームを下図で紹介する。水素分子の電子遷移は可視領域には存在せず、振動遷移も赤外活性ではないため直接吸収遷移は利用できない。そこで、インパルシブラマン遷移を利用して、 二色のレーザーの差周波を水素分子の振動遷移エネルギーに共鳴させることで、v=1←0遷移を誘起する手法をとった。実験では600nmのポンプパルスと800nmのストークスパルスを重ねることにより 振動遷移を引き起こしている。ヨウ素の場合と同様、遅延時間τ経過後に同じポンプ・ストークスパルス対を入射することで、二つの波束を重ね合わせることができる。 生成される状態は
のように表される。3節で紹介したヨウ素分子の場合と同様、励起パルス間の遅延時間τを変化させることによって、振動励起状態の振幅が変動していくことがわかる。 生成した波束の状態は遅延時間経過後にプローブパルスを入射して、そのパルスが散乱されて生じるアンチストークスパルスを観測することで行う。ポンプ・ストークスパルスで作成した コヒーレンスの状態をプローブパルスで観測するという手法はCARS(coherent anti-Stokes Raman scattering)の手法と全く同じである。 一連の実験のスキームを図示すると図4-2のようになる。
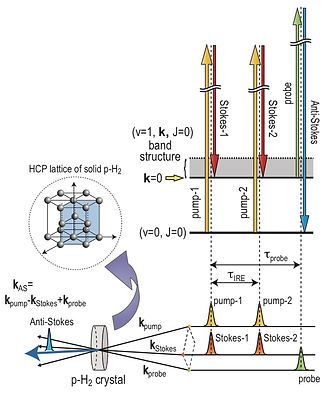

図4-3 パラ水素量子干渉フリンジ
図4-2 パラ水素実験のスキーム
振動波束の励起はインパルシブに起きるので、ポンプパルスとストークスパルスは時間的に重なっていることが必要である。 プローブパルスのタイミング(τprobe)を最初の励起パルスから1ns後ろのタイミングに固定しておいて、二回のラマン励起の間のタイミング(τIRE) を変化させた場合、2節で見た強め合いと弱め合いが交互に起きる様子が図4-3のように観測される。振動の周期はv=1とv=0状態のエネルギーの差からおよそ8fsと見積もられる。
実際に測定して得られたシグナルを下図に示す。二回の励起を重ねることで、相対強度は0から4の間で変動しており、非常に高い精度で波束の重ね合わせが制御できていることがわかる。また、固体中でのコヒーレンスの保持時間も非常に長く、500ps経過後においても 劣化の度合いは10%程度に抑えられていることがわかる。
4-2. 二次元位相変調器を用いた空間位相分布の制御
4-1の結果を元に、ポンプ・ストークスパルスの空間波面を二次元位相変調器によって制御することで、時間的な制御と空間的な干渉制御を同時に行い、 その結果をアンチストークスパルスの空間分布イメージとして読み出す手法を確立した。この結果、空間位相変調器を用いて自在な波面分布を作成して、 パラ水素結晶中に書き込むことで任意の位相分布が実現できる。デモンストレーションとして2x2のドットパターンを固体パラ水素中に書き込む実験を行った。 マスクのデザインにより、個々の4つのスポットに対し、任意の位相分布を書き込むことができる。 実際に4つのスポットに(0,0,0,0),(0,180,0,180),(0,270,180,90)という3つの位相情報を書き込み、その状態を読み出した結果を図4-4に示す。 それぞれのスポットの強度が異なる位相で振動していることがわかり、空間的な位相分布の書き込みと読み出しに成功している。

図4-4 空間位相分布の書き込み/読み出し実験
このような位相分布の観測を応用すれば、外部からの摂動による位相のずれや、固体中の不均一環境に由来する振動周期の違いなどを読み出すことも可能となる。
【関連論文】
-
Optically engineered quantum interference of delocalized wavefunctions in a bulk solid: The example of solid para-hydrogen
H. Katsuki, Y. Kayanuma, and K. Ohmori, Phys. Rev. B 88, 014507 (2013). -
Manipulation and visualization of two-dimensional phase distribution of vibrational wavefunctions in solid para-hydrogen crystal
H. Katsuki, K. Ohmori, T. Horie, H. Yanagi, and K. Ohmori, Phys. Rev. B, 92, 094511 (2015). -
Simultaneous manipulation and observation of multiple ro-vibrational eigenstates in solid para-hydrogen
H. Katsuki and K. Ohmori, J. Chem. Phys. 145, 124316 (2016).

