6. コヒーレントフォノン制御
固体結晶に対し、そのフォノン振動の周期よりも短い時間幅を持ったパルスレーザーを照射すると、結晶のフォノン運動を励起することができる。通常の熱で励起されるフォノンと異なり、 レーザー光が照射された領域内で原子(分子)の運動の位相が揃った状態で励起が行われるため、このようなフォノン振動をコヒーレントフォノンと呼ぶ。 コヒーレントフォノンを計測するには、pump-probe分光によって反射率の変化として計測することが一般的です。
6-1. ビスマス単結晶の二次元原子運動の制御と可視化
ビスマスの単位格子を図11に示す。z軸方向に振動するA1gモードとxy平面内で二重縮退したEgモードという二つのモードが存在して�いる。 これらのモードの励起振幅を光によって制御することができれば、結晶格子中の原子の運動を制御できることに繋がる。実験では、図12のような光学系を用い、ポンプ光の照射による プローブ光の反射率変化を測定している。

図11 ビスマスの単位格子とフォノンモード

図12 コヒーレントフォノン光学系
励起パルスとしてチャープパルスを時間的に重ねた励起パルスを用い、両者の遅延時間を制御することでTHz領域の変調をスペクトルに与え、フォノンの振幅制御をおこなっている。 さらにab initio計算によって反射率の変化と原子の変位の間の比例定数を計算し、反射率の変化から光の照射された平面内における原子の変位を可視化することに成功した。 より詳細を知りたい方は、以下の文献を参考にして下さい。
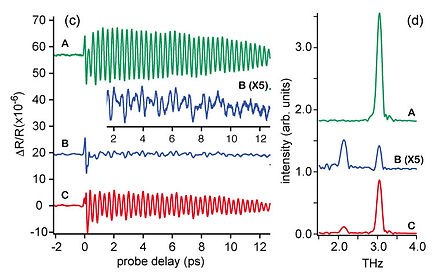
図13 フォノン振幅制御結果
6-2. ルブレン単結晶のTHzフォノン熱浴分布の制御
現在執筆中
【関連論文】
-
Optical manipulation of coherent phonons in superconducting YBa2Cu3O7-δ thin films
Y. Okano, H. Katsuki, Y. Nakagawa, H. Takahashi, K. G. Nakamura and K. Ohmori, Faraday Discussions 153, 375-382 (2011). -
All-Optical Control and Visualization of Ultrafast 2D Atomic Motions in a Single Crystal of Bismuth
H. Katsuki, J. C. Delagnes, K. Hosaka, K. Ishioka, H. Chiba, E. S. Zijlstra, M. E. Garcia, H. Takahashi, K. Watanabe, M. Kitajima, Y. Matsumoto, K. G. Nakamura, and K. Ohmori, Nature Communications 4:2801 doi:10.1038/ncomms3801 (2013). -
Mode Selective Excitation of THz vibrations in Single Crystalline Rubrene
K. Yano, H. Katsuki, and H. Yanagi,
J. Chem. Phys. 150, 054503 (2019).
5. 励起子ポラリトンのコヒーレント制御
光の波長程度の微小領域に閉じ込めた光と物質の励起子が混ざり合ってできる準粒子をマイクロキャビティ励起子ポラリトンと呼ぶ。その成り立ちから、この粒子は光と物質の特徴を併せ持った興味深い研究対象である。 現在、無機量子ドットを微小キャビティ中に閉じ込めてフォトンと結合させた系において、ポラリトン凝縮と呼ばれる原子のボーズアインシュタイン凝縮と類似した興味深い現象が観測されている。ポラリトン凝縮状態は量子的な状態であり、その状態からの発光は必然的にコヒーレントな光となるため、低しきい値でのレーザー発振(ポラリトンレーザー)が報告されており、今後の応用へ向けて研究が進んでいる。また、有機分子の励起子とフォトン からなる励起子ポラリトンも最近報告がなされ、新たな応用分野が広がりつつある。有機分子を利用したポラリトンは室温かつテーブルトップの環境で、いわば「ガラス1枚」の中でポラリトン凝縮という量子的な集団を実現できるため、今後の応用を考えた場合非常に魅力的である。
コヒーレント制御の観点から見た場合にも、励起子ポラリトンは非常に興味深い系である。その理由として、まず一つ目に有効質量が非常に小さいために光子との運動量のやり取りがダイレクトに 操作、観察できる系であるということ、二つ目にポラリトン凝縮に関連した自発的なコヒーレンスの生成という現象と外部からの光によるコヒーレンスの生成という、 相反する二つの事象を扱える可能性がある点である。
5-1. キャビティポラリトンの基礎
光を閉じ込めるキャビティにも様々な形態が存在しているが、我々が用いるのは分散型ブラッグ反射ミラーと呼ばれる高い反射率を持った2枚のミラーの間に活性媒質層をサンドイッチしたような構造である。このような平面キャビティに閉じ込められた光ではキャビティ軸に平行な面直方向の運動量が量子化される。この結果、そのエネルギーは

のように表される。一方、励起子のエネルギーEexは一定値をとると考えることができる。横軸に面内運動量k||、縦軸にエネルギーを取った時のこれらのプロットは図5-1の点線のようになる。ここで、キャビティ光子と励起子の間に相互作用が存在していると、エネルギー準位の変化が起きる。簡単のためCoupled Harmonic oscillator モデルを用いてこれらの励起子、キャビティ光子のハミルトニアン行列を記述すると、

図5-1 ポラリトンの分散曲線
と表される。ここでVは励起子-キャビティ光子間の相互作用を表す。この行列を対角化することで得られる固有状態は
と表される。本来は各準位の緩和時間に関するパラメータも関連してくるが、この取り扱いでは簡単のため無視している。この新たな状態の分散を図5-1に赤線で示してある。固有ベクトルを計算すれば、この状態は励起子成分とキャビティ光子の成分が混ざり合っていることがわかる。これが励起子ポラリトンと呼ばれる状態を表すのだが、Vの大きさがどんなものでもポラリトンと呼んで良いか、というとそういうわけではなく相互作用の大きさについての条件が課せられる。簡単にいうと、Vと励起子、光子の緩和係数Γex, Γphotonの間に
という関係が成り立つ場合を強結合状態とよび、この条件下で生成される新たな準粒子のことを励起子ポラリトンと呼ぶ。物理的には、分裂した2つのピークの間隔がそれぞれのピークの線幅よりも大きく、明確に観測できる条件に対応している。

