6. コヒーレントフォノン制御
固体結晶に対し、そのフォノン振動の周期よりも短い時間幅を持ったパルスレーザーを照射すると、結晶のフォノン運動を励起することができる。通常の熱で励起されるフォノンと異なり、 レーザー光が照射された領域内で原子(分子)の運動の位相が揃った状態で励起が行われるため、このようなフォノン振動をコヒーレントフォノンと呼ぶ。 コヒーレントフォノンを計測するには、pump-probe分光によって反射率の変化として計測することが一般的です。
6-1. ビスマス単結晶の二次元原子運動の制御と可視化
ビスマスの単位格子を図11に示す。z軸方向に振動するA1gモードとxy平面内で二重縮退したEgモードという二つのモードが存在して�いる。 これらのモードの励起振幅を光によって制御することができれば、結晶格子中の原子の運動を制御できることに繋がる。実験では、図12のような光学系を用い、ポンプ光の照射による プローブ光の反射率変化を測定している。

図11 ビスマスの単位格子とフォノンモード

図12 コヒーレントフォノン光学系
励起パルスとしてチャープパルスを時間的に重ねた励起パルスを用い、両者の遅延時間を制御することでTHz領域の変調をスペクトルに与え、フォノンの振幅制御をおこなっている。 さらにab initio計算によって反射率の変化と原子の変位の間の比例定数を計算し、反射率の変化から光の照射された平面内における原子の変位を可視化することに成功した。 より詳細を知りたい方は、以下の文献を参考にして下さい。
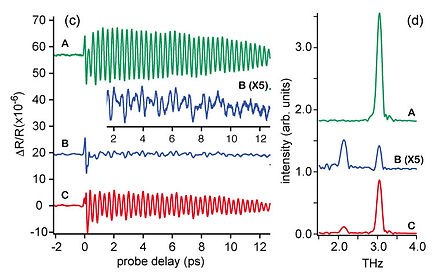
図13 フォノン振幅制御結果
6-2. ルブレン単結晶のTHzフォノン熱浴分布の制御
現在執筆中
【関連論文】
-
Optical manipulation of coherent phonons in superconducting YBa2Cu3O7-δ thin films
Y. Okano, H. Katsuki, Y. Nakagawa, H. Takahashi, K. G. Nakamura and K. Ohmori, Faraday Discussions 153, 375-382 (2011). -
All-Optical Control and Visualization of Ultrafast 2D Atomic Motions in a Single Crystal of Bismuth
H. Katsuki, J. C. Delagnes, K. Hosaka, K. Ishioka, H. Chiba, E. S. Zijlstra, M. E. Garcia, H. Takahashi, K. Watanabe, M. Kitajima, Y. Matsumoto, K. G. Nakamura, and K. Ohmori, Nature Communications 4:2801 doi:10.1038/ncomms3801 (2013). -
Mode Selective Excitation of THz vibrations in Single Crystalline Rubrene
K. Yano, H. Katsuki, and H. Yanagi,
J. Chem. Phys. 150, 054503 (2019).
4. Control of ro-vibrational WP in solid para-hydrogen
4-1. Amplitude control by nonlinear spectroscopic techniques
Here We go one step further and apply the coherent control to condensed phase system. Hydrogen molecule is classified into two species, para- and ortho-, based on the symmetry of the wavefunction. Due to the Pauri's exclusion principle, the rotational states with even(odd) quantum number can couple only with nuclear spin functions which is antisymmetric(symmetric) under the permutation of the hydrogen nucleus. The former is called para-hydrogen and the latter is called ortho-hydrogen. The inter-conversion between para and orthodox species is very slow without magnetic interactions. Under the low temperature (~5K), all the para-hydrogen occupies the J=0 state, which has the isotropic distribution. As a result, the para-hydrogen molecules in the J=0 state can be assumed like a rare-gas atom having a symmetric nuclear distribution (See Fig.7). These molecules have no permanent multipole moments, so that the intermolecular electrostatic interaction is very small. As for the pure vibrational transition of v=1←0, the coherence lifetime is extremely long (ns order). These characteristics offer an ideal testbed for the condensed phase coherent control experiments.

Fig.7 Structure of para-hydrogen crystal
The wavefunction of a para-hydrogen crystal can be built up from the molecular basis function. Consider a quantum state in which one molecule labelled i is excited to v=1 state and all the other molecules in the v=0 state. Such state is described as
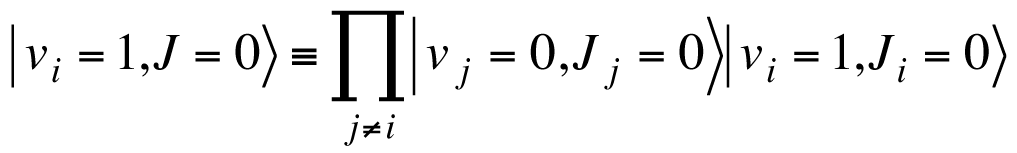
.
Taking these functions as basis sets, we calculate the intermolecular interaction. After diagonalizing the interaction matrix, we obtain delocalized vibrational eigenfunctions which are labelled by wave vector k as
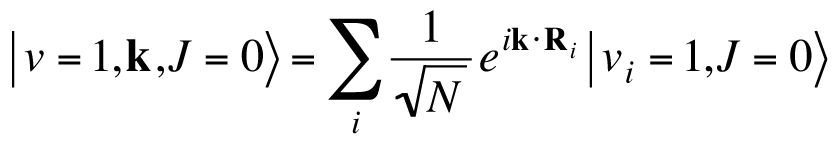
.
In this para-hydrogen crystal, we performed the wave packet interference experiments. The experimental scheme is depicted in FIg. 8. Since the para-hydrogen molecule is homonuclear, the vibrational state can be excited only through the Raman transition. We use two-color laser pulses, pump pulse at 600nm and Stokes pulse at 800nm, to impulsively excite the v=1 state. Similar to the gas phase experiments, two Raman excitation pulses are irradiated with the time delay τ. In this case, the generated wave packet state is described as
.
Similar to Chap.3, the amplitude of v=1 state oscillates with the frequency corresponding to the energy difference between v=0 and 1 states. Due to the selection rule of Raman transition, only k=0 state can be excited in an ideal crystal. The state of the wave packet can be probed by shining a probe pulse after temporal evolution. The scattered anti-Stokes pulse is detected by the set of spectrometer and CCD camera. Note that the detected anti-Stokes signal is a coherent radiation, so that the detection efficiency is much better than fluorescence detection in Chap. 3. The experimental scheme of Fig. 8 is very similar to the coherent anti-Stokes Raman scattering (CARS) spectroscopy, which is a third order nonlinear spectroscopy.
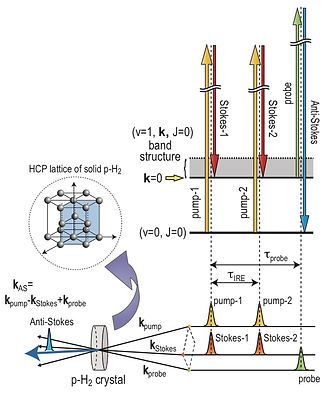
Fig.8 Scheme of nonlinear optical experiment utilized for coherent control in para-hydrogen crystal

Fig.9 Ramsey fringe observed for v=1←0 transition. The x axis corresponds to the delay between the first and second Raman excitation.
振動波束の励起はインパルシブに起きるので、ポンプパルスとストークスパルスは時間的に重なっていることが必要である。 プローブパルスのタイミング(τprobe)を最初の励起パルスから1ns後ろのタイミングに固定しておいて、二回のラマン励起の間のタイミング(τIRE) を変化させた場合、2節で見た強め合いと弱め合いが交互に起きる様子が図9のように観測される。振動の周期はv=1とv=0状態のエネルギーの差からおよそ8fsと見積もられる。
実際に測定して得られたシグナルを下図に示す。二回の励起を重ねることで、相対強度は0から4の間で変動しており、非常に高い精度で波束の重ね合わせが制御できていることがわかる。また、固体中でのコヒーレンスの保持時間も非常に長く、500ps経過後においても 劣化の度合いは10%程度に抑えられていることがわかる。
4-2. 二次元位相変調器を用いた空間位相分布の制御
4-1の結果を元に、ポンプ・ストークスパルスの空間波面を二次元位相変調器によって制御することで、時間的な制御と空間的な干渉制御を同時に行い、 その結果をアンチストークスパルスの空間分布イメージとして読み出す手法を確立した。この結果、空間位相変調器を用いて自在な波面分布を作成して、 パラ水素結晶中に書き込むことで任意の位相分布が実現できる。デモンストレーションとして2x2のドットパターンを固体パラ水素中に書き込む実験を行った。 マスクのデザインにより、個々の4つのスポットに対し、任意の位相分布を書き込むことができる。 実際に4つのスポットに(0,0,0,0),(0,180,0,180),(0,270,180,90)という3つの位相情報を書き込み、その状態を読み出した結果を図10に示す。 それぞれのスポットの強度が異なる位相で振動していることがわかり、空間的な位相分布の書き込みと読み出しに成功している。

