6. コヒーレントフォノン制御
固体結晶に対し、そのフォノン振動の周期よりも短い時間幅を持ったパルスレーザーを照射すると、結晶のフォノン運動を励起することができる。通常の熱で励起されるフォノンと異なり、 レーザー光が照射された領域内で原子(分子)の運動の位相が揃った状態で励起が行われるため、このようなフォノン振動をコヒーレントフォノンと呼ぶ。 コヒーレントフォノンを計測するには、pump-probe分光によって反射率の変化として計測することが一般的です。
6-1. ビスマス単結晶の二次元原子運動の制御と可視化
ビスマスの単位格子を図11に示す。z軸方向に振動するA1gモードとxy平面内で二重縮退したEgモードという二つのモードが存在している。 これらのモードの励起振幅を光によって制御することができれば、結晶格子中の原子の運動を制御できることに繋がる。実験では、図12のような光学系を用い、ポンプ光の照射による プローブ光の反射率変化を測定している。

図11 ビスマスの単位格子とフォノンモード

図12 コヒーレントフォノン光学系
励起パルスとしてチャープパルスを時間的に重ねた励起パルスを用い、両者の遅延時間を制御することでTHz領域の変調をスペクトルに与え、フォノンの振幅制御をおこなっている。 さらにab initio計算によって反射率の変化と原子の変位の間の比例定数を計算し、反射率の変化から光の照射された平面内における原子の変位を可視化することに成功した。 より詳細を知りたい方は、以下の文献を参考にして下さい。
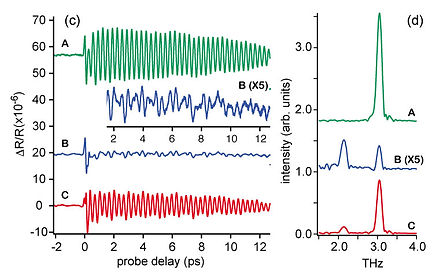
図13 フォノン振幅制御結果
6-2. ルブレン単結晶のTHzフォノン熱浴分布の制御
現在執筆中
【関連論文】
-
Optical manipulation of coherent phonons in superconducting YBa2Cu3O7-δ thin films
Y. Okano, H. Katsuki, Y. Nakagawa, H. Takahashi, K. G. Nakamura and K. Ohmori, Faraday Discussions 153, 375-382 (2011). -
All-Optical Control and Visualization of Ultrafast 2D Atomic Motions in a Single Crystal of Bismuth
H. Katsuki, J. C. Delagnes, K. Hosaka, K. Ishioka, H. Chiba, E. S. Zijlstra, M. E. Garcia, H. Takahashi, K. Watanabe, M. Kitajima, Y. Matsumoto, K. G. Nakamura, and K. Ohmori, Nature Communications 4:2801 doi:10.1038/ncomms3801 (2013). -
Mode Selective Excitation of THz vibrations in Single Crystalline Rubrene
K. Yano, H. Katsuki, and H. Yanagi,
J. Chem. Phys. 150, 054503 (2019).
2. What is Coherent Control?
Coherent control is a technique to manipulate the quantum wavefunction of atoms and molecules utilizing the coherent light sources. Through the light-matter interaction, the coherent characteristics of the light is imprinted on the wavefunctions of the target quantum system. The characteristics of the light, such as the temporal envelope and the spectrum, can be designed easily using the apparatus such as spatial light modulator and the Michelson interferometer. With such pulses, interference of wavefunctions can be manipulated so that the amplitude and phase distribution of the wavefunction can be controlled from outside.
In our research, the wavefunction of the target quantum system is manipulated by femtosecond ultrashort laser pulses. Our final goal is to control the macroscopic characteristics of the target system by the coherent control techniques. Coherent control can be applied for the photo-reaction branching ratio control, and is also an important building block to manipulate the qubit states which is indispensable for quantum computing and quantum information technology.
The most important characteristics necessary for the coherent control is the "long coherence life time." The photo-excited quantum state loses its quantum nature during the temporal evolution, due to the irreversible relaxation process called pure dephasing. Coherent control is effective only when the target system keeps the clear definition of the phase. If the phase is unclear, the interference doesn't bear any contrast.
For coherent control, we need a highly coherent light sources, i.e. lasers. In our group, we use femtosecond ultrashort laser pulses to perform coherent control. Femtosecond laser pulses have broad spectral bandwidth, so that it is also convenient to produce a wave packet, which is a linear combination of quantum eigenfunctions. For example, the vibrational wave packet generated in the electronic excited state is described as follows,
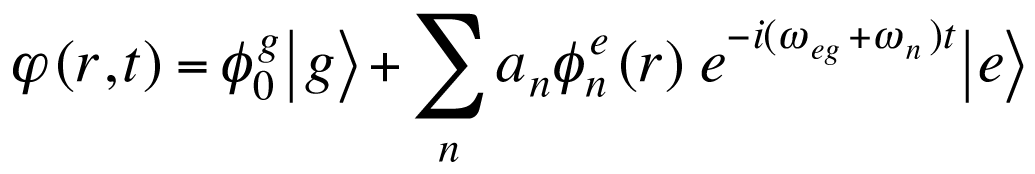
where Φ0g is a vibrational eigenfunction with v=0 in the ground state. Φne is the v=n state vibrational eigenfunction in the electronic excited state, ωeg is the transition angular frequency between the electronic ground and excited states, ωn is the vibrational angular frequency, an is the amplitude of v=n state, and |g> and |e> are the bra-ket notation of the electronic wave functions. Depend on the target quantum states, wave packet (WP) is called vibrational WP, electronic WP, rotational WP, etc.
In the following, I will mainly focus on the motion of vibrational WPs. What is shown below is the WP motion (probability distribution) in a 1D harmonic potential, where x-axis represents the internuclear distance. As you see, the motion of the packet is periodic, which is defined as classical vibrational period (Tvib). In realistic molecular potential, the potential is anharmonic so that the packet shows collapse and revival structure as temporal evolution.
Wave packet motion in a harmonic potential
Next, we consider the situation where a pair of time-delayed femtosecond(fs) laser pulses is shined on the molecule with delay τ. Assuming that the laser pulse intensity is not so strong so that the depletion of the ground state population is negligible, the WP is described as,
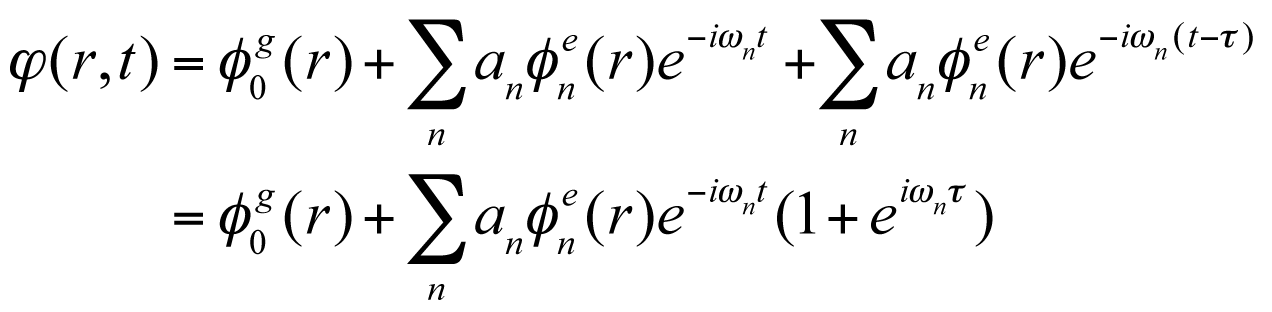
.
Squaring this equation gives the population distribution as
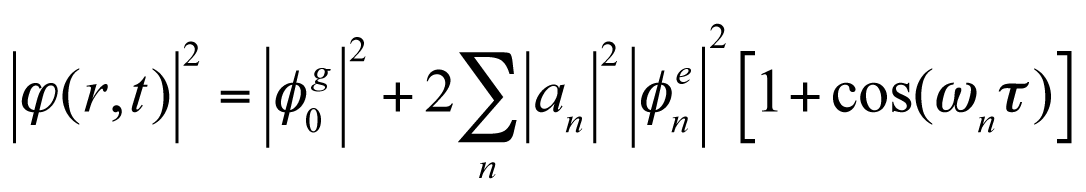
.
What is important in this equation is that the population oscillates as a function of τ with the angular frequency of ωn. For the gas phase iodine molecule, the electronic transition is performed with 530 nm pump wavelength, corresponding to the oscillation period of 1.8×10 s. This indicates that very accurate manipulation of the delay timing τ is necessary for the control of population distribution. The following figures show the result of WP simulation at constructive and destructive timings.
-15
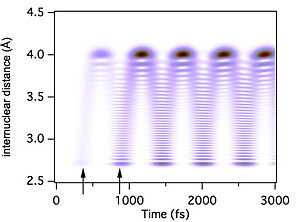
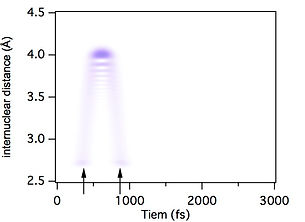
Fig.2 (a) Constructive overlap of two WPs
Fig.2 (b) Destructive overlap of two WPs
The black vertical arrows indicate the timing of laser irradiation. Hereafter, we call the first laser pulse as pump pulse, and second laser pulse as control pulse. The delay τ is set to 499.7fs and 498.8fs for Fig. 2(a) and (b), respectively. Note that the timing shift of only 0.9 fs results in the drastic difference of the WP motion. In an ideal situation without decoherence, the population oscillates between 0 and 4 for each eigenstate.
In my research, I'm interested in the coherent control of various levels of quantum systems. For simple systems such as gas phase isolated molecules, the coherent control is more straightforward. However, this also means that the results are "easily imaginable by the simulations." Now I'm facing more complex many body quantum systems such as molecular crystals and strong coupling systems. Fig. 3 is the overview of various kinds of quantum systems I'm interested in. In the following, I will introduce the coherent control experiments in each quantum system. If you are not familiar with this field, I recommend to start with gas phase systems, which is a good demonstration of coherent control.
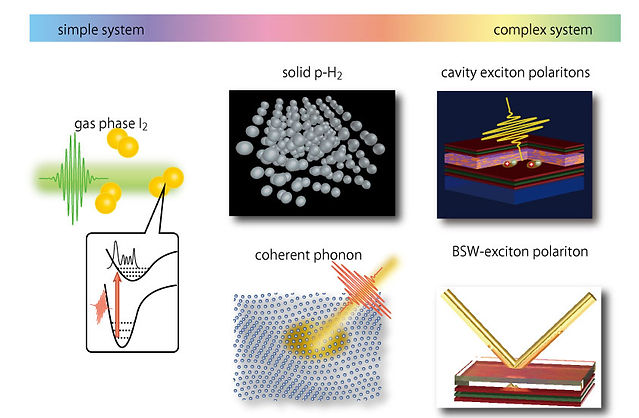
Fig.3 Various kinds of quantum systems to be handled by coherent control

